Once Marcus du Sautoy asked Sir Andrew Wiles what he’d scribble in the margin he’d proved to tease next generation. Answer: congruent number problem
A congruent number is a positive integer that is the area of a right triangle with three rational number sides.
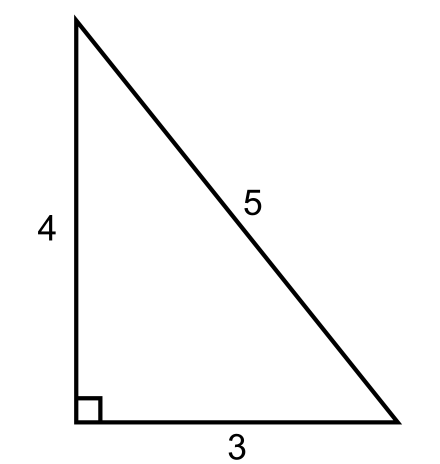
\(
\displaystyle
\begin{matrix}
a^{2}+b^{2}&=&c^{2},\\
\frac{1}{2}ab&=&n.
\end{matrix}
\)
\(
\displaystyle
\begin{matrix}
a^2 = c^2 - b^2 \\
2a^2 + 2ac = a^2 + c^2 + 2ac - b^2 \\
2ab(a+c) = b(a+c)^{2} - b^{3} \\
4n(a+c) = b(a+c)^{2}-b^{3} \\
\frac{4n(a+c)}{b^4} = \frac{(a+c)^{2}}{b^{3}}-\frac{1}{b} \\
\frac{4n^{4}(a+c)^{2}}{b^{4}} = \frac{n^{3}(a+c)^{3}}{b^3}-\frac{n^3(a+c)}{b} \\
(\frac{2n^2(a+c)^2}{b^2})^{2} = (\frac{n(a+c)}{b})^{3} - n^{2}(\frac{n(a+c)}{b}) \\
set \hspace{1mm} y = \frac{2n^2(a+c)}{b^2}, \\
x = \frac{n(a+c)}{b} \\
y^2 = x^3 - n^2x
\end{matrix}
\)
n is a congruent number if and only if the elliptic curve \( y^2 = x^3-n^2x \) contains a rational point with \( y \neq 0 \)
\(
\displaystyle
\begin{matrix}
x = \frac{n(a+c)}{b} = \frac{n(c+a)(c-a)}{b(c-a)} = \frac{nb}{c-a} \\
y = \frac{2n^2(a+c)}{b^2} = \frac{2n^2(a+c)}{c^2-a^2} = \frac{2n^2}{c-a} \\
\frac{x}{y}=\frac{b}{2n} \\
b = \frac{2nx}{y}, \\
a=\frac{2a^2+2ac}{2(a+c)} \\
=\frac{a^2+2ac+a^2}{2(a+c)} \\
=\frac{a^2+2ac+c^2-b^2}{2(a+c)} \\
=\frac{(a+c)^2-b^2}{2(a+c)} \\
=\frac{n^2(a+c)^2-b^2n^2}{2n^2(a+c)} \\
=\frac{(\frac{n(a+c)}{b}^{2}-n^2}{\frac{2n^2(a+c)}{b^2}} \\
=\frac{x^2-n^2}{y}, \\
c=\frac{2c(a+c)}{2(a+c)} \\
=\frac{2c^2+2ac}{2(a+c)} \\
=\frac{a^2+c^2+2ac+c^2-a^2}{2(a+c)} \\
=\frac{(a+c)^2+c^2-a^2}{2(a+c)} \\
=\frac{(a+c)^2+b^2}{2(a+c)} \\
=\frac{n^2(a+c)^2+b^2n^2}{2n^2(a+c)} \\
=\frac{(\frac{n(a+c)}{b})^2+n^2}{\frac{2n^2(a+c)}{b^2}} \\
=\frac{x^2+n^2}{y}
\end{matrix}
\)
We have a bijection(one-to-one correspondence)
\(
\Large
\{(a,b,c) \in \mathbb{Q}^{3} \mid a^2+b^2=c^2,\frac{ab}{2}=n \} \leftrightarrow \{(x,y) \in \mathbb{Q}^{2} \mid y^2 = x^3-n^2x \hspace{1mm} and \hspace{1mm} y \neq 0 \}
\)
with inverse functions
\(
\Large
(a,b,c) \mapsto (\frac{nb}{c-a},\frac{2n^2}{c-a}) \hspace{8pt} and \hspace{8pt} (x,y) \mapsto (\frac{x^2-n^2}{y},\frac{2nx}{y},\frac{x^2+n^2}{y})
\)
\( y^2 = x^3-25x \) has rational point \( x=-4, y= \pm 6 \), 5 is a congruent number.
\(
\begin{align*}
\begin{cases}
a = \frac{-4^2-5^2}{-6} = \frac{3}{2} \\
b = \frac{2\times5\times-4}{-6} = \frac{20}{3} \\
c = \frac{-4^2+5^2}{6} = \frac{41}{6}
\end{cases}
\end{align*}
\)
\( y^2 = x^3-36x \) has rational points
\(
\displaystyle
\begin{matrix}
x=-3,\hspace{1mm} y= \pm 9, \\
x=-2,\hspace{1mm} y= \pm 8, \\
x=12,\hspace{1mm} y= \pm 36, \\
x=18,\hspace{1mm} y= \pm 72, \\
\end{matrix}
\),
6 is a congruent number.
\(
\begin{align*}
\begin{cases}
a = \frac{12^2-6^2}{36} = 3 \\
b = \frac{2\times6\times12}{36} = 4 \\
c = \frac{12^2+6^2}{36} = 5
\end{cases}
\end{align*}
\)
- One very old problem concerned with rational points on elliptic curves is the congruent number problem. One way of stating it is to ask which rational integers can occur as the areas of right-angled triangles with rational length sides. Such integers are called congruent numbers. … It is closely related to the problem of determining the rational points on the curve \( C_n : y^2 = x^3 − n^2x \). … As an example of this, consider the conjecture of Euler from 1769 that \( x^4 + y^4 + z^4 = t^4 \) has no non-trivial solutions. By finding a curve of genus 1 on the surface and a point of infinite order on this curve, Noam Elkies found the solution \( 2682440^4 + 15365639^4 + 18796760^4 = 20615673^4\) . His argument shows that there are infinitely many solutions to Euler’s equation. – The Birch And Swinnerton-Dyer Conjecture, by Andrew Wiles