free photos website
command
1 | open -a "Google Chrome" index.html |
My English Words List - April - 2023
unscathed
adjective
She escaped from the wreckage unscathed.
detest
verb
I detest pepperoni, and wouldn’t eat it if you paid me!
prank
noun
He enjoys playing pranks on his friends.
verb
Do not prank me!
ventilation
noun
a room with good ventilation
headphone
noun
earphone
noun
earbud
noun
scrapbook
noun
scrounge
verb
scrounge a dollar from a friend
sprout
verb
seeds sprouting in the spring
The garden is sprouting weeds.
splinter
noun
I got a splinter in my finger.
There were splinters of glass everywhere.
sprinkle
verb
He sprinkled water on the plants.
noun
splatter
verb
Rain splattered against the windows.
sprawl
verb
The kids sprawled on the floor to watch TV.
sprawled on the couch watching TV
The bushes were sprawling along the road.
jackpot
noun
The lottery jackpot is up to one million dollars.
blockbuster
noun
the movie is expected to be the biggest blockbuster of the summer
jackal
noun
phantom
noun
The crisis is merely a phantom made up by the media.
cartwheel
noun
- a large coin (such as a silver dollar)
chili
noun
- a hot pepper
rip
verb
She ripped the fabric in half.
He ripped open the package.
chant
verb
protesters were chanting outside
rant
verb
- to talk loudly and wildly
gripe
verb
The students griped that they had too much homework.
rune
noun
mope
verb
Like a little child, he often moped when he didn’t get what he wanted.
twine
noun
The package was wrapped in brown paper and tied with twine.
robe
noun
The priest wore a purple robe.
gape
verb
- to open the mouth wide
rage
verb
She raged about the injustice of their decision.
dude
noun
Hey, dude, what’s up?
OK, dude, whatever you say.
benevolent
adjective
a benevolent donor
a benevolent society
a benevolent organization
benevolent smiles
sage
noun
mane
noun
- long and heavy hair growing about the neck and head of some mammals (such as horses and lions)
The lion’s mane
slime
noun
Green slime covers the surface of the pond.
vie
verb
vied with his colleagues for the coveted promotion
marinate
verb
The recipe says that you should marinate the chicken overnight.
chew
verb
We were taught to chew our food thoroughly before swallowing.
You’re not allowed to chew gum in class.
fondue
noun
dip fruit in melted chocolate to have a chocolate fondue
borough
noun
A borough is an administrative division in various English-speaking countries. In principle, the term borough designates a self-governing walled town, although in practice, official use of the term varies widely.
frown
verb
She was frowning when she entered the room, so I knew that she was annoyed about something.
scowl
Noun
The teacher gave me a scowl when I walked in late.
Beethoven’s iconic scowl
growl
verb
the dog growled at the stranger
boil
verb
a pot of boiling water
pout
verb
a pouting child
The boy didn’t want to leave—he stomped his feet and pouted.
howl
verb
several coyotes began howling close by as the sun went down
slouch
noun
The difference between the slouch and standing straight up, was the difference between a negative and positive perception.
verb
The boy was slouching over his school books.
prowl
verb
a tiger prowling in the jungle
The police were prowling the streets in their patrol cars.
I prowled the store looking for sales.
rowdy
adjective
a rowdy game of basketball
turquoise
noun
The Landlord's Tale. Paul Revere's Ride
Listen, my children, and you shall hear
Of the midnight ride of Paul Revere,
On the eighteenth of April, in Seventy-five;
Hardly a man is now alive
Who remembers that famous day and year.
He said to his friend, “If the British march
By land or sea from the town to-night,
Hang a lantern aloft in the belfry arch
Of the North Church tower as a signal light,—
One, if by land, and two, if by sea;
And I on the opposite shore will be,
Ready to ride and spread the alarm
Through every Middlesex village and farm,
For the country folk to be up and to arm.”
Then he said, “Good night!” and with muffled oar
Silently rowed to the Charlestown shore,
Just as the moon rose over the bay,
Where swinging wide at her moorings lay
The Somerset, British man-of-war;
A phantom ship, with each mast and spar
Across the moon like a prison bar,
And a huge black hulk, that was magnified
By its own reflection in the tide.
Meanwhile, his friend, through alley and street,
Wanders and watches with eager ears,
Till in the silence around him he hears
The muster of men at the barrack door,
The sound of arms, and the tramp of feet,
And the measured tread of the grenadiers,
Marching down to their boats on the shore.
Then he climbed the tower of the Old North Church,
By the wooden stairs, with stealthy tread,
To the belfry-chamber overhead,
And startled the pigeons from their perch
On the sombre rafters, that round him made
Masses and moving shapes of shade, —
By the trembling ladder, steep and tall,
To the highest window in the wall,
Where he paused to listen and look down
A moment on the roofs of the town,
And the moonlight flowing over all.
Beneath, in the churchyard, lay the dead,
In their night-encampment on the hill,
Wrapped in silence so deep and still
That he could hear, like a sentinel’s tread,
The watchful night-wind, as it went
Creeping along from tent to tent,
And seeming to whisper, “All is well!”
A moment only he feels the spell
Of the place and the hour, and the secret dread
Of the lonely belfry and the dead;
For suddenly all his thoughts are bent
On a shadowy something far away,
Where the river widens to meet the bay, —
A line of black that bends and floats
On the rising tide, like a bridge of boats.
Meanwhile, impatient to mount and ride,
Booted and spurred, with a heavy stride
On the opposite shore walked Paul Revere.
Now he patted his horse’s side,
Now gazed at the landscape far and near,
Then, impetuous, stamped the earth,
And turned and tightened his saddle girth;
But mostly he watched with eager search
The belfry-tower of the Old North Church,
As it rose above the graves on the hill,
Lonely and spectral and sombre and still.
And lo! as he looks, on the belfry’s height
A glimmer, and then a gleam of light!
He springs to the saddle, the bridle he turns,
But lingers and gazes, till full on his sight
A second lamp in the belfry burns!
A hurry of hoofs in a village street,
A shape in the moonlight, a bulk in the dark,
And beneath, from the pebbles, in passing, a spark
Struck out by a steed flying fearless and fleet:
That was all! And yet, through the gloom and the light,
The fate of a nation was riding that night;
And the spark struck out by that steed, in his flight,
Kindled the land into flame with its heat.
He has left the village and mounted the steep,
And beneath him, tranquil and broad and deep,
Is the Mystic, meeting the ocean tides;
And under the alders, that skirt its edge,
Now soft on the sand, now loud on the ledge,
Is heard the tramp of his steed as he rides.
It was twelve by the village clock,
When he crossed the bridge into Medford town.
He heard the crowing of the cock,
And the barking of the farmer’s dog,
And felt the damp of the river fog,
That rises after the sun goes down.
It was one by the village clock,
When he galloped into Lexington.
He saw the gilded weathercock
Swim in the moonlight as he passed,
And the meeting-house windows, blank and bare,
Gaze at him with a spectral glare,
As if they already stood aghast
At the bloody work they would look upon.
It was two by the village clock,
When he came to the bridge in Concord town.
He heard the bleating of the flock,
And the twitter of birds among the trees,
And felt the breath of the morning breeze
Blowing over the meadows brown.
And one was safe and asleep in his bed
Who at the bridge would be first to fall,
Who that day would be lying dead,
Pierced by a British musket-ball.
You know the rest. In the books you have read,
How the British Regulars fired and fled, —
How the farmers gave them ball for ball,
From behind each fence and farm-yard wall,
Chasing the red-coats down the lane,
Then crossing the fields to emerge again
Under the trees at the turn of the road,
And only pausing to fire and load.
So through the night rode Paul Revere;
And so through the night went his cry of alarm
To every Middlesex village and farm, —
A cry of defiance and not of fear,
A voice in the darkness, a knock at the door,
And a word that shall echo forevermore!
For, borne on the night-wind of the Past,
Through all our history, to the last,
In the hour of darkness and peril and need,
The people will waken and listen to hear
The hurrying hoof-beats of that steed,
And the midnight message of Paul Revere.
Prime Number（素数，质数）
Who would have imagined that something as straightforward as the natural numbers (1, 2, 3, 4,…) could give birth to anything so baffling as the prime numbers (2, 3 ,5, 7, 11, …)?
—— Ian Stewart
素数的分布
The ‘average’ distribution of primes is very regular; its density shows a steady but slow decrease. On the other hand the distribution of the primes in detail is extremely irregular. (G.H.Hardy)
God may not play dice with the universe, but something strange is going on with the prime numbers. (Carl Pomerance/Paul Erdős)
The prime number theorem shows that the primes have some large-scale structure, even though they can behave quite randomly at smaller scales.(Terence Tao)
On the other hand, the primes also have some local structure. For instance,(Terence Tao)
- They are all odd (with one exception);
- They are all adjacent to a multiple of six (with two exceptions);
- Their last digit is always 1, 3, 7, or 9 (with two exceptions).
素数的随机分布
在整体上表现出正则性倾向而在局部却呈现出无规则性态，这是素数分布的一个值得注意的地方。
素数就像对物理学家极其重要的“理想气体”，客观地讲，其分布可以说是确定的，然而当我们试图描述它在一给定点的情况时，我们却观察到类似掷骰子碰运气的赌博那样的统计振荡。
素数如同理想气体那样占据着所能允许的整个空间（而这正意味着随机性），也就是说，素数在那些非常严格使之极端正则的限制性条件下有着充分的自由度。
在大多数关于素数的猜想中都隐含着这样的观点：任何不是显然不可能的实际都是可实现的。（Les Nombres Premiers）
素数之美
我们可以用相当好的准确度来预测N以内素数的个数.另一方面，素数在一些短区间内的分布是相当没有规律的。这种既“随机”又可预测相组合便使得素数的分布既是有序的排列，同时又有意外的现象。Schroeder在他精彩的书《科学和通信中的数论》(1984)一书中，把这种现象称作是艺术作品的基本要素。许多数学家都认为素数分布问题具有极大的美学动力。(The little book of bigger primes)
重要事实
The series \(\sum \frac{1}{p} = \frac{1}{2} + \frac{1}{3} + \frac{1}{5} \dots \) is divergent. 而\( \sum_{n=1}^{\infty}\frac{1}{n^2} = \frac{\pi^2}{6} \)，这说明质数是正整数集的真正有份量的子集
Euler product
\(\displaystyle {\begin{aligned}\prod _{p,\in ,\mathbb {P} }\left({\frac {1}{1-{\frac {1}{p^{s}}}}}\right) = \sum _{n=1}^{\infty }{\frac {1}{n^{s}}}.\end{aligned}}\)
holds for all s such that the left-hand side converges absolutely.
\( \sum _{n≤x} {\frac{1}{n}} = \log x + \gamma + O(1/x) \)
where \( \gamma \) is Euler-Mascheroni constant.
\( \gamma=0.577215664901532860651…. \)
\( \sum _{p≤x} {\frac{1}{p}} = \log \log x + B_1 + O(\frac{1}{\log x}) \)
where \( B_1 \) is Mertens constant.
\( B_1=0.2614972128… \).
Brun’s Constant
The number obtained by adding the reciprocals of the odd twin primes, \( B≡(1/3+1/5)+(1/5+1/7)+(1/11+1/13)+(1/17+1/19)+… \), By Brun’s theorem, the series converges to a definite number, which expresses the scarcity of twin primes, even if there are infinitely many of them.
B≈1.902160583104
The logarithmic function
\(log x \) tends to infinity more slowly than any positive power of x.
\(\frac{log x}{x^δ} → 0 \) for every positive δ.
The function \( \frac{x}{log x} \) tends to infinity more slowly than x but more rapidly than \( x^{1-δ} \), and it is the simplest function which has this property.
The Prime Number Theorem
The number of primes not exceeding x is asymptotic to \( \frac{x}{log x} \).
The nth prime is approximately equal to \( nln n \).
\( \displaystyle \pi (x)\sim {\frac {x}{\log x}} \).
\( \displaystyle \pi (x)\sim \operatorname {Li} (x)=\int _{2}^{x}{\frac {dt}{\log t}}=\operatorname {li} (x)-\operatorname {li} (2). \)
Riemann hypothesis is equivalent to
\( \displaystyle \pi (x)=\operatorname {Li} (x)+O\left({\sqrt {x}}\log x\right) \)
\( \forall \varepsilon > 0, \pi (x)=\operatorname {Li} (x)+O(x^{\frac{1}{2}+ε}) \)
Observe that
\( \displaystyle \pi (x) \) greater than the ‘logarithm integral’ \( \operatorname {Li} (x) \) depends upon the largeness of \( log log log x \) for large x.
John Edensor Littlewood found that the sign of the difference \( \pi (x)-\operatorname {Li} (x) \) changes infinitely often.
Any prime number,except 2 or 3,is 6n+1 or 6n+5.
素数与混沌
素数表显示了素数的混沌特性，而其表面的无序性最终却与一些，比如说源于物理现象的经典随机模型相吻合。
完全随机即混沌具有无穷大的复杂度；另一方面，整数的复杂度显然是随其大小的增加而增大；在无穷远处，整数序列表现出随机的性状，因而素数序列也蕴涵着随机性。(Les Nombres Premiers)
素数-随机-混沌
Probabilistic number theory: different prime numbers are, in some serious sense, like independent random variables.
Dynamical: the prime numbers were seen to be moving particles in a 1-dimensional continuum
Cramér & 模1一致分布: 素数序列看起来就像一个受同样增长性约束的随机序列
素数似乎达到了他们所能被允许的随机性的极限。
素数的整体分布参数不足以用来描述它们局部的不规则性。
Euler as Bach of Math
Mathematicians have tried in vain to this day to discover some order in the sequence of prime numbers, and we have reason to believe that it is a mystery into which the mind will never penetrate. - Leonard Euler
Gauss as Mozart of Math
The problem of distinguishing prime numbers from composite numbers and of resolving the latter into their prime factors is known to be one of the most important and useful in arithmetic. It has engaged the industry and wisdom of ancient and modern geometers to such an extent that it would be superfluous to discuss the problem at length…Further, the dignity of the science itself seems to require that every possible means be explored for the solution of a problem so elegant and so celebrated. - G.F.Gauss
Sieve
Terence Tao
The sequence of primes behaves “unpredictably” or “randomly”, we do not have a (useful) exact formula for the nth prime number pn!
Despite not having a good exact formula for the sequence of primes, we do have a fairly good inexact formula as Prime number theorem.
The von Mangoldt function(as an analogy, sound wave) which is noisy at prime number times, and quiet at other times.
Fourier transforms is just like listenning to this wave and record the notes that you hear (the zeroes of the Riemann zeta function, or the “music of the primes”). Each such note corresponds to a hidden pattern in the distribution of the primes.
The infamous Riemann hypothesis predicts a more precise formula for pn, which should be accurate to an error of about \( \sqrt n \).
If the Riemann hypothesis is true, we can remove one exponential.
Interestingly, the error \( O(\sqrt n ㏑^3 n) \) predicted by the Riemann hypothesis is essentially the same type of error one would have expected if the primes were distributed randomly. (The law of large numbers)
Thus the Riemann hypothesis asserts (in some sense) that the primes are pseudorandom - they behave randomly, even though they are actually deterministic.
The type of pseudorandomness properties which underlie cryptographic protocols are not the same as the type of pseudorandomness properties which underlie conjectures such as the Riemann hypothesis; thus for instance a solution to the Riemann hypothesis would be a dramatic event in pure mathematics, but would not directly impact cryptographic security.
Sieves study the set of primes in aggregate, rather than trying to focus on each prime individually.
The sieve now captures not only primes, but also almost primes - numbers with very few prime factors.
We are still unable to detect several types of patterns in the primes. However, we have made recent progress on one type of pattern, namely an arithmetic progression.
I actually haven’t thought seriously about RH since some very naive attempts at it in graduate school. It’s possible that one could approach this problem by finding out more structure in the zeta function, but my (somewhat uninformed) opinion is that zeta is inherently a rather pseudorandom object (except of course for its obvious structural properties such as meromorphicity, asymptotics, and the functional equation), and it may be better to return to the prime number side of things, for instance by locating a new proof of the prime number theorem, or finding a way to exclude Siegel zeroes and obtain a more effective prime number theorem in arithmetic progressions. But it’s hard to see how current methods can hope to get the type of power gain in the error terms for prime statistics which would be needed for the full RH; some radically new idea would be needed for that, probably. - see http://terrytao.wordpress.com/2008/01/07/ams-lecture-structure-and-randomness-in-the-prime-numbers, AMS lecture: Structure and randomness in the prime numbers
aesthetics
The music of the primes is a chord?
Atle Selberg: If anything at all in our universe is correct, it has to be the Riemann hypothesis, if for no other reasons, so for purely esthetical reasons. The simple ideas are the ones that will survive.
J. Brian Conrey: RH tells us that the primes are distributed in as nice a way as possible. If RH were false, there would be some strange irregularities in the distribution of primes; the first zero off the line would be a very important mathematical constant. It seems unlikely that nature is that perverse!
Enrico Bombieri: The failure of the Riemann hypothesis would create havoc in the distribution of prime numbers.
Marcus du Sautoy: As we shall see, Riemann’s Hypothesis can be interpreted as an example of a general philosophy among mathematicians that, given a choice between an ugly world and an aesthetic one, Nature always chooses the latter.
References
- Structure and Randomness in the prime numbers.ppt, Terence Tao
- A small selection of results in number theory.pdf, Terence Tao
- 素数论，法国科普丛书知否第571卷Les Nombres Premiers，姚家燕译
- An Introduction to the Theory of Numbers, G.H.Hardy & E.M.Wright
- Prime Obsession - Bernhard Riemann and the Greatest Unsolved Problem in Mathematics, John Derbyshire
- 博大精深的素数，P.Ribenboim
- http://www.secamlocal.ex.ac.uk/people/staff/mrwatkin
- http://mathworld.wolfram.com
My English Words List - March - 2023
diarrhea
noun
The symptoms of the disease include fever, nausea, and diarrhea.
norovirus
noun
Norovirus, the culprit behind a nasty stomach bug, is rising again in Canada
vomit
verb
clean up after someone with Norovirus vomits or has Diarrhea
noun
Vomit and poop can splatter in all directions
clean up must be very thorough to not miss any drops of vomit or poop you can’t see.
e-commerce
noun
- commerce conducted via the Internet
prompt
noun
person creates a prompt
artifact
noun
generative AI generates a noval artifact
ethic
noun
strong work ethics
congest
verb
traffic congested the highways
congested streets
hypotenuse
noun
- the side of a right-angled triangle that is opposite the right angle
convex
adjective
- curved or rounded outward like the exterior of a sphere or circle
convex lenses are used to correct for farsightedness
concave
adjective
- hollowed or rounded inward like the inside of a bowl
flip
verb
flip a coin
flip a pancake
bland
adjective
a bland smile
bland diet
nugget
noun
chicken nuggets
pavilion
noun
picky
adjective
a picky eater
blush
noun
at first blush
The fruit is yellow, with a blush of pink.
braid
verb
She braids her hair every morning.
noun
until she was 15, she had a braid that reached to her knees
copywriter
noun
a writer of advertising or publicity copy
aromatic
adjective
aromatic herbs
aromatic flowers can add greatly to the ambience of a room
deafening
adjective
the deafening roar of the planes
The deafening thunder frightened all the children.
coleslaw
noun
- a salad made of raw sliced or chopped cabbage
Coleslaw is the correct spelling for the cabbage-based side salad often served alongside barbecue.
Be Brave, But Be Careful
Reporter: Why did you want to climb Mount Everest?
George Mallory: Because it’s there
Those famous words were spoken by British climber George Mallory in 1923, by the time he was interviewed for the New York Times.
Mallory’s body was eventually found in 1999, on the north face of the mountain.
George Pólya: If you want to climb the Matterhorn, you might first wish to go to Zermat, where those who have tried are buried.
I will make it
Keep going west
Fifty years ago a physician sailed across the Atlantic, unassisted, in a kayak to test the stresses on the human body and see if it was possible to survive for long periods at sea. It was a voyage that nearly killed him. His voyage made world headlines and showed him it was possible to survive for long periods at sea. Lindemann was by no means the first person to cross the Atlantic alone, but his feat was one of the most daring crossings in history.
In 1957 Lindemann published a best-selling book Alone at Sea
My First Memory (of Librarians)
This is my first memory:
A big room with heavy wooden tables that sat on a creaky
wood floor
A line of green shades—bankers’ lights—down the center
Heavy oak chairs that were too low or maybe I was simply
too short
For me to sit in and read
So my first book was always big
In the foyer up four steps a semi-circle desk presided
To the left side the card catalogue
On the right newspapers draped over what looked like
a quilt rack
Magazines face out from the wall
The welcoming smile of my librarian
The anticipation in my heart
All those books—another world—just waiting
At my fingertips.
- My First Memory (of Librarians)
- I, that used to figure Paradise In such a library’s guise. – Poema de los dones - Poem about gifts by Jorge Luis Borges
My English Words List - February - 2023
engagement
noun
We have a dinner engagement this weekend.
gut
noun
- the basic visceral, emotional, or instinctual part of a person
Consult more than one financial adviser before making a final choice, and trust your gut.— Quentin Fottrell
My gut says this is, overall, a terrible idea.— Erica Buist
a gut feeling
Your gut can help you determine which decision suits you best.
adjective
a gut reaction
phobia
noun
His fear of crowds eventually developed into a phobia.
mutism
noun
Social phobia (SOP) and selective mutism (SM) are related anxiety disorders characterized by distress and dysfunction in social situations. SOP typically onsets in adolescence and affects about 8% of the general population, whereas SM onsets before age 5 and is prevalent in up to 2% of youth.
slit
noun
- a long narrow cut or opening
You could see through the slit in the fence.
verb
I slit the bag open at the top.
reanimate
verb
It seems better to reanimate the contents learned yesterday before acquiring new ones.
azure
noun
- the blue color of the clear sky
supernova
noun
- superstar
What Lights the Universe’s Standard Candles?
Type Ia supernovas are astronomers’ best tools for measuring cosmic distances.
frigid
adjective
- freezing cold
The frigid gusts of wind stung their faces.
The temperature there is a frigid -400 degrees Fahrenheit—colder than the surface of Pluto, and just a tad warmer than absolute zero. — Katrina Miller, WIRED, 13 Dec. 2022
vilify
verb
He was vilified in the press for his comments.
banyan
noun
terrain
noun
Terrain affects surface water flow and distribution. Over a large area, it can affect weather and climate patterns.
We hiked through a variety of terrains.
succumb
verb
They will pressure you, and you must try not to succumb.
Older people are more likely to succumb to the ravages of COVID-19. — Mary Kekatos, ABC News, 19 Nov. 2022
ingrain
verb
ingrain young children with responsibility
It is in our homes and classrooms that lifelong attitudes are ingrained.
The Sun (2007)
Each day we make countless choices and live out deeply ingrained habits that all add up to a lifestyle.
Christianity Today (2000)
adjective
ingrain carpet
ensnare
verb
The animals got ensnared in the net.
The police successfully ensnared the burglar.
blunder
noun
- a bad or stupid mistake
The accident was the result of a series of blunders.
fixed a minor blunder in the advertising flyer
bust
verb
He busted his watch when he fell.
Two students got busted by the teacher for smoking in the bathroom.
noun
boom and bust
knack
noun
- a natural ability : talent
She has a knack for telling interesting stories.
has a knack for making friends
attest
verb
I can attest that what he has said is true.
the result attests the truth of that statement
hallway
noun
Her office is at the end of the hallway.
A hallway or corridor is an interior space in a building that is used to connect other rooms. Hallways are generally long and narrow.
hypocrite
noun
Bill Gates gets ‘called out’ for being a ‘climate hypocrite’
Bill Gates has confronted accusations that he is a “hypocrite” as he uses his private jet while he is campaigning for technologies designed to support global efforts to tackle climate change.
pawpaw
noun
- papaya
flatware
noun
thicket
noun
buoyancy
noun
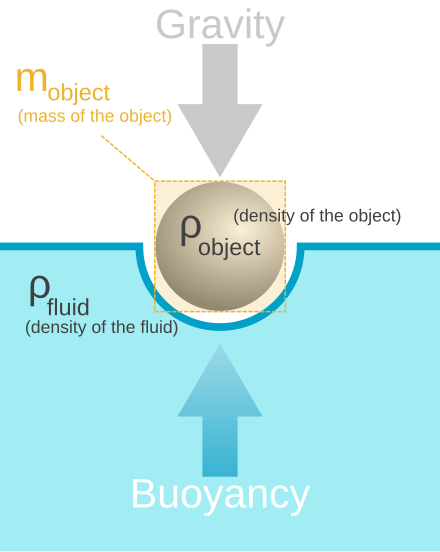
the buoyancy of a cork in water
the buoyancy of seawater
The swimmer is supported by the water’s buoyancy.
rapport
noun
He quickly developed a good rapport with the other teachers.
There is a lack of rapport between the members of the group.
The Snow Man
One must have a mind of winter
To regard the frost and the boughs
Of the pine-trees crusted with snow;
And have been cold a long time
To behold the junipers shagged with ice,
The spruces rough in the distant glitter
Of the January sun; and not to think
Of any misery in the sound of the wind,
In the sound of a few leaves,
Which is the sound of the land
Full of the same wind
That is blowing in the same bare place
For the listener, who listens in the snow,
And, nothing himself, beholds
Nothing that is not there and the nothing that is.
Today is Very Boring
Today is very boring,
It’s a very boring day,
There is nothing much to look at,
There is nothing much to say,
There’s a peacock on my sneakers,
There’s a penguin on my head,
There’s a dormouse on my doorstep,
I am going back to bed.
Today is very boring,
It is boring through and through,
There is absolutely nothing
That I think I want to do,
I see giants riding rhinos,
And an ogre with a sword,
There’s a dragon blowing smoke rings,
I am positively bored.
Today is very boring,
I can hardly help but yawn,
There’s a flying saucer landing
In the middle of my lawn,
A volcano just erupted
Less than half a mile away,
And I think I felt an earthquake,
It’s a very boring day.
- Spotlight Poetry - Today is Very Boring - A poem by Jack Prelutsky
- The mind is its own place, and in itself Can make a heav’n of hell, a hell of heav’n. (John Milton, Paradise Lost)